カーネル法

ディープラーニングが現れる以前の機械学習で一斉を風靡した学習機械と言えばSupport Vector Machine(SVM)ですね。このSVMが大活躍した背景には、線形回帰・分離の手法を非線形へ拡張するカーネル法の存在がありました。

今回はそのカーネル法について解説します。

機械学習における非線形な問題の基本的な考え方は、線形では扱えなさそうなデータに対して変換を施して、その変換先で線形な処理ができるようにすることです。

ではそのような上手い変換はいかにして獲得されるのでしょう。その変換先での空間の次元はいくつにすべきでしょう。様々な問題が浮上しますが、カーネル法では陽に変換の具体的な形を扱うことなく、内積演算(すなわちスカラー値)だけによって問題を解決します。

ニューラルネットでは上手い変換を学習によって獲得するため、高い表現能力を得る一方、学習の時点で多大なる時間を要するのが問題でした。

非線形回帰・分離の基本的な考え方
カーネル法
識別の問題、SVMへの応用
- SVMの解法
まとめ

非線形回帰・分離の基本的な考え方

まずは線形分離の例を見てみましょう。

クラス1のデータが赤、クラス2のデータが青のときに分離直線を以下のように引けます。

f:id:s0sem0y:20160522212549p:plain

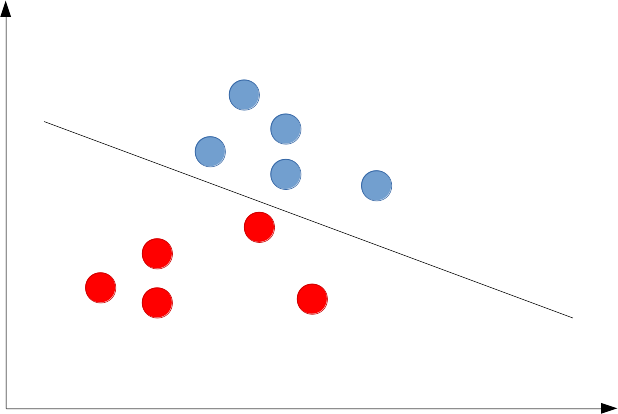
はたして分離直線の位置(切片)や傾きはこれでいいのかという問題があります。パーセプトロン学習は、ともかく分離できる直線を適当に見つけ出し、SVMの場合は分離にきわどいデータ点からなるべく離れるように直線が引かれます。これらは個々の手法で詳しく学んでください。

今回着目すべきは、データ点が直線では分離できないような場合に、どのように問題を解決するかということです。こういう場合は、下図左のように2次元のデータ点 $x_n$ (この図ではデータ点が15個なので $n=1,...,15$ )が得られた場合に、これを適当な非線形変換 $φ(x_n)$ によってデータ点を変換してしまい、具合の良い変換であれば右図のように、クラス毎に固まった場所にデータ点が写ってくれます。よって変換先の新しい平面では線形分離ができそうです。

回帰の問題も基本的には同じで、データ点が直線上に配置されていないなというときに、データ点を変換してしまい、変換後の空間で直線を引きます。

f:id:s0sem0y:20160522213416p:plain f:id:s0sem0y:20160522213556p:plain

これらの手続きをすると、変換後の空間での直線は、元の空間に戻ってきたら曲線になっているので、結果だけ見れば、もとのデータ点にたいして曲線により回帰・分類を行ったことになります。

カーネル関数

カーネル法にとって最も重要なのはカーネル関数と呼ばれる内積演算に相当する関数です。

カーネル関数 $k()$ は2つのデータ点 $x,x'$ に対して以下で定義されます。

$k(x,x')=φ(x)^Tφ(x')$

です。ここで $φ()$ はデータ点を変換する都合の良い関数です。今は、そのような関数 $φ$ が見つかっているものとして考えてください。カーネル法ではこのカーネル関数が後々に重要な役割を担います。

回帰問題の例

基本的な線形回帰の問題を例に見て行きましょう。

普通の重回帰の問題であれば、データ $x$ に対して、重みベクトル $w$ を使い、 $y=w^Tx$ によって回帰をしたいという問題です。いまは、データを適当な変換 $φ$ によって変換して、その値を使って回帰をしようとしているので、 $y=w^Tφ(x)$ によって回帰することを考えます。

例として、いろいろな部屋の $x=(温度,体積)_n$ に対して $t_n=圧力_n$ のデータが複数あるとき、これらの関係を知りたい場合に回帰を使います。つまり $y=w^Tφ(x)$ というのは各 $x_n$ に対して、回帰線上の点 $y_n$ がなるべく $t_n$ に近づくように決められるべきです。

つまり、

$J(w)=\frac{1}{2} \sum_{n=1}{N} \left( w^Tφ(x_n)-t_n \right)^2$

を最小化するように $w$ を決定します。オーバーフィッティングを避けるために正則化という手法が使えますから、今回は正則化項 $\frac{λ}{2}w^Tw$ を用いて

$J(w)=\frac{1}{2} \sum_{n=1}{N} \left( w^Tφ(x_n)-t_n \right)^2+\frac{λ}{2}w^Tw$

を最小化します。正則化についての効用は以下の記事を参照してください。

s0sem0y.hatenablog.com

問題を同値な別の表現へ：双対問題

$J(w)=\frac{1}{2} \sum_{n=1}^{N} \left( w^Tφ(x_n)-t_n \right)^2+\frac{λ}{2}w^Tw$

を $w$ について最小化すべく $w$ について $J(w)$ を微分し、 $J'(w)=0$ となる $w$ を探します。まず $J'(w)=0$ は以下となります。

$\sum_{n=1}^{N} \left( w^Tφ(x_n)-t_n \right)φ(x_n)+λw=0$

通常はこれを $w$ について解いて、解を求めたいということですが、これを以下のように式変形していきます。

$w=-\frac{1}{λ} \sum_{n=1}^{N} \left( w^Tφ(x_n)-t_n \right)φ(x_n)$

ここで、 $a_n=-\frac{1}{λ} \left( w^Tφ(x_n)-t_n \right)$ として、そのベクトルを $a=(a_1,...,a_N)^T$ と置き、

$w= \sum_{n=1}^{N}a_nφ(x_n)=Φ^Ta$

と表現します。ここで、 $Φ$ は $φ(x_n)T$ を $n$ 行目に持つ行列です。

ともかく $w=Φ^Ta$ は元々の $J(w)$ を最小化するために、微分して $0$ と置いたときに出てきた式です。この $w$ を $J(w)$ 代入すると

$J(w)=J(a(w))=\frac{1}{2}a^TΦΦ^TΦΦ^Ta-a^TΦΦ^Tt+\frac{1}{2}t^Tt+\frac{λ}{2}a^TΦΦ^Ta$

となります。ただし $t=(t_1,...,t_N)$ です。

やけに $Φ^TΦ$ がたくさん出てくるので、この行列を $K=Φ^TΦ$ と置きます(N✕N行列になっている)。

このとき $K$ の $i$ 行 $j$ 列の成分はカーネル関数 $k(x_i,x_j)$ となっています。この $K$ を使って $J(a)$ を表現し直すと

$J(a)=\frac{1}{2}a^TKKa-a^TKt+\frac{1}{2}t^Tt+\frac{λ}{2}a^TKa$

と書くことができます。

この考えのメリット

$w= \sum_{n=1}^{N}a_nφ(x_n)=Φ^Ta$

$a_n=-\frac{1}{λ} \left( w^Tφ(x_n)-t_n \right)$

これらから、 $w$ を消去してしまえば

$a=(K+λI_N)^{-1}t$

となる。これを線形回帰のモデルに代入し直すと

$y(x)=w^Tφ(x)=a^TΦφ(x)=k(x)^T(K+λI_N)^{-1}t$

と得られる。新しいデータ $x$ に対する予測値は上記の式にデータを代入すればいいことになります。これのメリットは、もはや回帰式はカーネル関数によってのみ完全に表現されていることです。具体的な非線形基底関数 $φ(x)$ を取り扱う必要はなく、 $k(x,x')=φ(x)^Tφ(x')$ という値についてのみ考えれば良くなっています。これは非線形基底関数がどれだけ次元が高かろうが、（事実上無限次元だろうが）取り扱えるということです。一旦データを違う空間に写像することで、その写像先で線形回帰をしようという発想だったのが、カーネル法では、写像先を具体的に考えられない無限次元などでも写像を直接取り扱わずにその効用を得られるのです。

識別の問題、SVMへの応用

s0sem0y.hatenablog.com

前回の記事で、SVMへの基礎を説明しました。

サポートベクターマシンはマージン最大化という観点で、データを識別する上手い境界線（識別面）を決める手法です。

SVMの解法

$t_n(w^Tφ(x_n)+w_0)\geq 1$

のもとで

$arg \min_{w,w_0} \frac{1}{2}|w|^2$

を解き、識別面 $y=w^Tφ(x)+w_0$

を決定することができます。上記の数式の導出は前回記事で行っています。

まずは双対問題を導くことです。非負のラグランジュ定数 $a=(a_1,...,a_N)^T$ を導入してラグランジュ関数を

$L(w,w_0,a)=\frac{1}{2}|w|^2-\sum_{n=1}^{N}a_n \left(t_n(w^Tφ(x_n)+w_0)-1 \right)$

とします。 $w$ と $w_0$ それぞれについて微分して0と置いた式が、条件式になりそれぞれ以下のように得られます。

$w=\sum_{n=1}^{N}a_nt_nφ(x_n)$

$0=\sum_{n=1}^{N}a_nt_n$

これをラグランジュ関数に戻すことで、以下の式の最大化問題になります。

$L(a)=\sum_{n=1}^{N}a_n-\frac{1}{2}\sum_{n=1}^{N}\sum_{m=1}^{N}a_na_mt_nt_mk(x_n,x_m)$

制約条件は以下です。

$a_n \geq 0$

$\sum_{n=1}^{N}a_nt_n=0$

これが双対表現で、最大化問題はまたしてもカーネル関数によって表現されました。これはラグランジュ定数 $a$ に対する最大化問題になっており、この二次計画問題を解いて $a$ を決めれば良いのです。

$w=\sum_{n=1}^{N}a_nt_nφ(x_n)$

を使えば、元々の識別平面の式は

$y=w^Tφ(x)+w_0=\sum_{n=1}^{N}a_nt_nφ(x_n)^Tφ(x)+w_0=\sum_{n=1}^{N}a_nt_nk(x,x')+w_0$

となります。結局双対問題で $a$ を決定したあとは、新しいデータ $x$ について上記の式 $y(x)$ の符号を調べれば識別ができるというわけです。（ $x_n$ は訓練データですから、実際には具体的に識別面が $x$ の関数で決まっています）

まとめ

回帰でも識別でも、一次関数では通用しないときに、データを $φ(x)$ で非線形写像して、その写像先で線形問題にしてしまうことを考えます。しかし、様々な非線形写像を試す際にはやけに高次元な、強いては無限次元への写像を考えると便利なことも多いです。

そのような場合に実際にその写像を計算することなく、しかしその効果だけを上手にいただく方法がカーネル法です。その肝はカーネル関数 $k(x,x')=φ(x)φ(x')$ というスカラー関数を考えることです。スカラー関数を考えてしまえば、事実上無限次元だろうが、計算するときには何も関係ありません。

そして、そうであるならば、わざわざ非線形写像 $φ(x)$ から考えずともカーネル関数 $k(x,x')$ を適当に作ってしまうところからスタートしてもいいはずです。これは非線形写像を作るよりもずっと簡単です。

具体的な理解を深めるためにはサポートベクターマシンの判定方法を手計算をして追ってみましょう。

s0sem0y.hatenablog.com