HELLO CYBERNETICS

深層学習、機械学習、強化学習、信号処理、制御工学、量子計算などをテーマに扱っていきます

状態空間表現と現代制御について基本的な考えを抑える

制御工学

　

　

follow us in feedly

f:id:s0sem0y:20170324035456p:plain

 

線形システムのモデル

状態空間表現

状態空間表現の主役

状態空間表現は、状態変数x(t)と入力u(t)、出力y(t)を用いて以下の連立微分方程式で記述されます。ボールド体は用いていませんが、基本的に小文字はベクトルであり大文字は行列ということで話を進めます。

 

{\dot x}(t) = Ax(t)+Bu(t)　,　x(0)=x_0

 

y(t)=Cx(t)+Du(t)

 

x_0は状態変数の初期状態です。

このモデルの第一式は、現在の入力変数と状態変数に依存して、状態変数の変化率が決定することを表しており、変化率が分かれば、時間tが進んだ時の状態変数の値が分かることになります。

 

第二式は、現在の状態変数の値と入力の値によって出力が決定されることを表しており、第一式を考慮すれば、状態変数の時間的な変化によって出力も時間的変化をするということになります。入力変数は方程式から導出されるのではなく、利用者側が決めるものであり、モデルの振る舞いを決める重要な変数になります。

 

出力と入力が1次元であればSISO(Single Input Single Output)と表現されます。出力と入力が多次元であればMIMO(Multi Input Multi Output)と表現されます。他にもSIMOやMISOなどの形式があり、それぞれ入出力の次元に対して言及しています。

 

特殊な状態空間表現、オートノマス系

上記で述べた状態空間表現の基本的なモデルで、入力を必要としない形式をオートノマス系と言います。

 

{\dot x}(t) = Ax(t)　,　x(0)=x_0

 

y(t)=Cx(t)

 

これは、状態変数の初期状態によって状態変数の変化率が決まり、これにより状態変数の振る舞いを決定することができます。その状態変数の振る舞いによって出力を決めることができ、これは連立微分方程式を上から順に解くことで、完全に振る舞いを知ることができる単純なモデルです。

 

ブロック線図による表現

状態空間表現のブロック線図

状態空間表現

 

{\dot x}(t) = Ax(t)+Bu(t)　,　x(0)=x_0

 

y(t)=Cx(t)+Du(t)

 

の第一式について、時間積分することで

 

x(t) =\displaystyle \int_0^t \{Ax(τ) + Bu(τ) \}dτ + x(0)

 

と状態変数x(t)を求めることができます。(右辺は各時間の状態変数、入力変数の値を全て足し合わせた値と、初期状態の値の和となっています)

状態変数x(t)が求まることで

 

y(t)=C\left( \displaystyle \int_0^t \{Ax(τ) + Bu(τ) \}dτ + x(0) \right)+Du(t)

 

とできるため、状態空間表現の出力について必要なのは初期状態と、入力変数であり以下のように簡潔に表すことができます。

 

f:id:s0sem0y:20170324024753p:plain

 

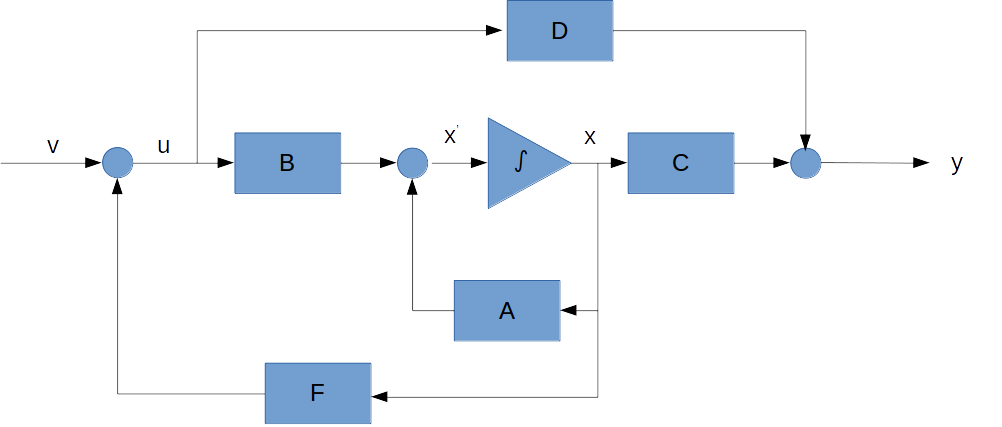
基本的なブロック線図を用いた状態空間表現

他にも基本的な演算をブロック線図で表現するために以下の形式が準備されています。

 

  • 乗算器：f_2=Kf_1

    f:id:s0sem0y:20170324025505p:plain




  • 積分器：f_2(t) = \displaystyle \int_0^t f_1(τ)dτ + f_2(0)


    f:id:s0sem0y:20170324025538p:plain



  • 加算器：f_3 = f_1 + f_2 


    f:id:s0sem0y:20170324025636p:plain

 

これらの基本的なブロック線図を用いて、状態空間モデルを記述すると以下の形になります。

 

{\dot x}(t) = Ax(t)+Bu(t)　,　x(0)=x_0

 

y(t)=Cx(t)+Du(t)

 

⇔

 

y(t)=C\left( \displaystyle \int_0^t \{Ax(τ) + Bu(τ) \}dτ + x(0) \right)+Du(t)

 

 

f:id:s0sem0y:20170324030710p:plain

 

 

線形システムを一度このように抽象的に記述してしまえば、電気系であろうが機械系であろうが関係なくシステムの振る舞いを理解することができます。

 

制御への応用

古典制御でのフィードバック制御

制御の目的は出力yを目標値に近づけるための入力xを設計することです。古典制御では基本的に入出力の値のみに着目します。最も単純なフィードバック制御の方法は、出力と目標値との偏差から、出力が目標値に近づくような新たな入力値を制御器に提案してもらい、出力を調整していくというものです。

 

この場合ブロック線図は以下のような形をしており、システムの内部について議論することはありません。

 

f:id:s0sem0y:20170318081154p:plain

 

このシステムに相当する部分を状態空間表現で表しておけば、以下の形式で表現することができます。

 

f:id:s0sem0y:20170324032950p:plain

このような入出力の値にのみ注目した制御方法である場合には、あまり状態空間モデルが役立つことはないかもしれません。

 

 

PID制御

制御工学で最も大成していると言えるPID制御はフィードバック制御の一種であり、多くの産業分野で応用されています。

 

s0sem0y.hatenablog.com

 

PID制御は古典制御の一種であり、制御器に相当する部分がPID制御器によって実現されています。PID制御器は偏差に比例した値、偏差の積分に比例した値、偏差の微分に比例した値を使って入力を定めます。

 

f:id:s0sem0y:20170318082345p:plain

(Wikipedia)

 

当然この制御方式を取る場合にも状態空間表現はあまり実るのある成果は出さないでしょう。

現代制御では、状態空間表現を有効に活用して制御する方法を提案します。

 

状態フィードバック

状態変数を入力までフィードバックする方法です。

この方法は状態空間表現でなければ実現できません。実用上状態変数を観測できなければならないことには注意が必要です。例えば、\dot xが加速度でxが速度である場合、速度を計測できる環境でなければ値をフィードバックすることはできません。

 

 

f:id:s0sem0y:20170324035456p:plain

 

このようなフィードバックの形式をいつでも数式と関連付けることができます。

 

{\dot x}(t) = Ax(t)+Bu(t)=Ax(t)+B(v(t)+Fx(t))=(A+BF)x(t)+Bv(t)　,　x(0)=x_0

 

y(t)=Cx(t)+Du(t)=Cx(t)+D(v(t)+Fx(t))=(C+DF)x(t)+Dv(t)

　

上記において最右辺は、あたかも新しい入力v(t)を使った状態空間表現のようにみなすことができます。つまり状態空間表現に状態フィードバックを用いることは、状態空間表現の入力を変更し、入力x(t)の係数行列を変更する機能を有していることになります。

 

状態フィードバックを使わない場合は以下の形式になっていることに注意。

 

{\dot x}(t) = Ax(t)+Bu(t)　,　x(0)=x_0

 

y(t)=Cx(t)+Du(t)

 

状態フィードバックを使うと、

u(t)→v(t)、A→A+BF、C→C+DF

に変更されている。

 

 

これにより通常の状態空間表現では、応答性や安定性に不具合がある場合に、それを(Fをうまく調整することで)修正する術を得たということです。 

出力注入

出力値を状態空間表現で表されたブロック線図の途中に挿入する方法です。

 

f:id:s0sem0y:20170324034634p:plain

 

このようなモデルを考えた後、いつでもこれを数式に戻すことができます。

 

{\dot x}(t) = Ax(t)+Bu(t)+Ky(t)　,　x(0)=x_0

 

y(t)=Cx(t)+Du(t)+w(t)

 

こちらは実は簡単には綺麗に持っていけませんが、w(t)を消去することで

 

{\dot x}(t) = (A-KC)x(t)+(B-KD)u(t)+Ky(t)　,　x(0)=x_0

 

と表せます。こちらは、状態フィードバックのように状態変数を観測する必要はなく、必要なのは出力の値だけです。つまりセンサをシステムの内部に入れておく必要がありません。

 

x(t)を観測できない時には状態フィードバックができないという話でした。

しかし上記のシステムにより、出力の値を観測し出力注入をすることで、状態変数の値を計算で求めることができます。

直接センサで状態変数を拾えない時、このような状態変数を計算により求められるシステムを構成することで、ここで得られる状態変数(の推定値)を使ってフィードバックを行うのです。

 

通常、このような状態変数を推定するためのシステムをオブザーバ(状態観測器)と呼びます。

 

 

現代制御のポイント

状態変数の概念導入

システムを入出力関係にのみ着目していた古典制御から、状態変数まで意識するように進化しました。それにより、更に正確に制御を行えるようになりました。

 

数式上で制御の可能性を議論

実は1つのシステムと1つの状態空間表現は1対1に対応しません。

1つのシステムに対して複数の状態空間表現が存在します。それは、状態空間表現に対して、両辺何らかの行列を掛けても、その行列に逆行列が存在する限り(正則である限り)戻ってくることができるためです。これを逆手に取り、更にシステムの議論を行いやすくする表現を獲得することもできます。

 

また、今回は状態フィードバックやオブザーバにより、システムを制御する方法を紹介しましたが、実際には、必ずしも制御ができるとも、状態変数の観測ができるとも限りません。

 

通常、制御できるか否かの性質を可制御性と言い、状態変数を観測できるか否かを可観測性と言い、これを議論するための可制御標準系や可観測標準系と呼ばれる状態空間表現があります。これらを用いて、マスマティカルに制御器の設計を行うことが可能です。

 

外乱への対策

実システムは常に何らかの外乱に曝されています。これに対応するような制御を行うことも考えられており、その成果として最適レギュレータがあります(通常の状態フィードバックでは持続的な外乱に対する対応作が考えられていなかった)。

 

また、オブザーバもシステムに生じる外乱に曝されており、正しく状態変数を推定できない可能性があります。その場合は、状態変数が確率的外乱によって乱されているとして、モデル化し、状態変数を推定するカルマンフィルタが使われます。これは現代制御の父と呼ばれるカルマンの名を冠した代表的な成果であり、多くの分野で応用されています。

 

ポスト現代制御へ

カルマンフィルタや最適レギュレータによって、システムが正確に記述されている場合に外部から外乱が生じた時の対応作は考えることができました。しかし、実システムはそもそも正確に微分方程式で表すことができるでしょうか。

 

微分方程式は例えばメカトロ系では、回路の抵抗値やインダクタンス、機械システムの剛性値や空気抵抗を必要とします。これらを完全に把握できている保証はあるでしょうか。

外部の外乱も含め、これらの微分方程式に組み込まれた値にズレがある場合にでも制御性能を担保する必要があり、これを解決すべくロバスト制御理論が考案されています。

 

また、抵抗値は熱に依存し、それは稼働時間に依存します。このように何らかの要因でシステムが時間的に変動するようなケースにおいて、制御器が自身の振る舞いを変えていく適応制御なども研究されています。

 

参考文献

 

線形システム解析 (システム制御工学シリーズ)

線形システム解析 (システム制御工学シリーズ)

 

 

 

線形ロバスト制御 (8) (計測・制御テクノロジーシリーズ)

線形ロバスト制御 (8) (計測・制御テクノロジーシリーズ)

 

 

 

s0sem0y

スポンサーリンク

コメントを書く