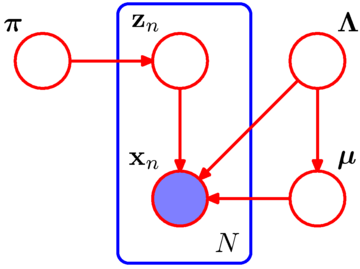
混合ガウスモデル
混合ガウスモデルは、複数のガウス分布を重ねあわせたものです。
混合ガウスモデルは、ガウス分布1つ1つをデータの発生源であると考え、そこから生起したデータを1つの塊、すなわちクラスターと見ることで、クラスタリングに応用することができます。
今回は混合ガウスモデルを用いたクラスタリングを、今年公開された確率プログラミングライブラリであるedwardを使って実装してみます(と言っても、サンプルを少しいじっただけだが)。
クラスタリングの結果
はじめに混合ガウスモデルを用いたクラスタリングが、どのような結果を出してくれるのかを見てしまいたいと思います。
以下がその結果を表す図です。

左がデータです。このデータは実際には5つのガウス分布から生起させたものであり、各データ点が色分けされて真ん中の図で表してあります。もちろん、こんな色分けができるのは、人工的なデータだからであり、元々データの発生源を知っているからです。
本来は左の図のデータが出てきた時、これがいくつのクラスターに分かれるのか(すなわちデータ発生源のガウス分布がいくつあるのか)ということは分かりません。
右は混合ガウス分布を使ってクラスタリングを行った結果です。しっかりと5つのクラスターを捉えられているのが分かります(ただし色の対応に意味はありません)。
ここで注目すべきなのは、まず学習は教師なしで行われるということ(クラスタリングなので当然ですが)。そして、仮定した混合ガウスモデルは、10個のガウス分布があると仮定していることです。
混合ガウス分布の概要
混合ガウス分布は以下で表されます。
簡潔に述べればガウス分布が
の重みで足し合わされているモデルということになります。ここで以下
が満たされていなければなりません。これは自体を確率と見なすためです。
学習とクラスタリング
データに対してこのモデルを上手くフィッティング(学習)させ、各ガウス分布の平均と分散、そしてを推定することで、各データ点が個々のどの分布から生起したのかを確率で表すことができるようになります。
それにより、各データ点を確率が高いガウス分布から生起したと見なすことでクラスタリングが可能になります。単にどのクラスタであるのかをハードに決めてしまうのではなく、確率という形で表現しているため、あまりにも信頼の薄いデータに対しては保留してしまうなどの対処も可能になります。
学習の方針
潜在変数の導入
確率的なモデルの学習は、数式はかなり難しそうに見えてしまうため、概要だけ述べます。
本来データはある特定の分布から生成したはずであり、それを表現する潜在変数
を導入します。は仮定されたガウス分布の個数である
次元のベクトルです。仮に
番目のガウス分布された場合、
番目の成分である
のみが
となり、他の成分は
となります。
そして、になるというのは
番目のガウス分布から生起したことを表し、この確率を
だとします。すなわち
です。そうなると
と表せます。右辺に関して、の殆どは
であるため、
となり、唯一
となっている
についてだけ
となります。当然、
であり、左辺についても、
番目の要素のみが
となっている確率変数ベクトル
の確率となり一致します。
ここでは確率変数です。データが生成される過程というのは、あるガウス分布が選ばれ(
が発生)、そのガウス分布から更にデータが発生(
が発生)と考えることができます。従ってデータの生成モデルは
と表すことができます。ちなみにこの数式のもとでを
について周辺化した場合は以下となり、
混合ガウス分布に対して、どの分布から生起したかを表すを明示的に組み込めたことになります。
負担率(事後確率)
次に、「負担率」なる確率変数を導入します。負担率は
であり、データが発生した時に、
となる確率を表しています。負担率は要するにデータが実際に得られた時に、そのデータがどのガウス分布から生起したのかを確率(事後確率)で教えてくれるということです。
パラメータのフィッティング(学習)
パラメータは基本的にはや
など、ガウス分布の平均と分散になります。更には
も必要となってきます。
通常このような確率的なモデルは、最尤推定によってパラメータを求めます。データが手元にあるわけですから、そのようなデータが生起するような確率(尤度)が最大になるようにパラメータを決めるというわけです。
しかし混合ガウス分布の最尤推定は解析的には綺麗に得られません(だいたいディープが流行っている今や殆どのモデルは解析的には求まらん)。
1.解決の方法としては、最適化手法としては勾配法(ニューラルネット御用達)やEMアルゴリズム(観測できない変数がある場合の一般的解法)があります。
2.他の方針として解析的には求まらない部分を近似する変分ベイズ法(平均場近似など物理学に基づく近似法)などがあります。
3.また、解析的には求まらない部分は大抵期待値の形をしているため、期待値を単純に標本平均とみなして、コンピュータで何個かデータを擬似的に発生させるサンプリング法(MCMC法など)による近似もあります。
プログラム
結果再訪
再びクラスタリングの結果を見ます。

・左が「5個」のガウス分布から発生させたデータ
・真ん中がどのガウス分布から発生したかを色分けしたもの
・右が「10個」のガウス分布からなる混合ガウス分布を仮定してクラスタリングを行った結果
となります。色が対応していないのは、10個のガウス分布を用いた際に、何番目のガウス分布のパラメータを配列の何番目に置くかはランダムだからです(matplotlib.scatterのカラーを配列の番号で指定している。そうですサボりました)。
クラスターの数を多めに見積もっておいて良い
まずポイントとして、クラスターの数を多めに見積もってしまっても構いません。むしろ少なく見積もるとそれ以上のクラスターに分けられなくなるので可能性が狭まります。
多めにとっても良いのは、推論の過程で、10個のガウス分布のうち不要なガウス分布は負担率が非常に小さく見積もられるからです(あるいは)。従って、事後分布でクラスターを推定する場合に、不要なガウス分布から生成された確率はかなり小さくなり、選ばれなくなります。
逆にはデータの生成確率を記述していたものであり、生成モデルからすれば、そもそもこの分布からはほとんどデータが出てきませんよ、と言っていることになります。
解法
学習にはギブスサンプリングを用いた近似を利用しています。
また上記の説明では通常の混合ガウス分布ですが、パラメータに対して事前分布を仮定しています(にはディリクレ分布、
にはガウス分布、
には逆ガンマ分布)。
コードの全体
生成したデータは共分散行列が対角行列になっています。
データは2次元で、分布の個数は5個です。全部で500点生成しています。
仮定したクラスタ(ガウス分布)の個数は10個です。
実際に準備したガウス分布の平均は
[1, 1]
[-1, -1]
[-1, 0.7]
[1, -0.8]
[0, 0]
のです。推定された10個のクラスタの平均は以下であり、準備したガウス分布を捉えていると考えらます(model.qpi.eval()の値を見れば分布が選ばれる確率も見られる)。
[ 0.02025411 0.09191971]
[-1.06901896 0.73215121] = [-1, 0.7]
[ 0.08771218 0.05939405]
[-0.99043369 -1.02555299] = [-1, -1]
[ 0.02464557 0.00551013]
[-0.02189424 0.0109568 ] = [0, 0]
[ 1.00027573 1.03204417] = [1, 1]
[ 1.06481922 -0.85521406] = [1, -0.8]
[ 0.02913276 0.06211369]
[ 0.0347905 0.02282866]
他のパラメータを持つ分布は明らかに生成確率が少なかったので無視された分布ということになるでしょう。適当にクラスターを多めに見積もってしまうというのは、要するにパラメータが無駄に増えることであり、下手したら過学習(仮定したモデルに無理矢理合わせる)の可能性も出るわけですが、ベイズの良いところはこういう部分は自動的に避けられるところにあるのでしょう。
最後に
感想
ディープラーニングで得られたパラメータは大抵よくわからんので、こういう手法はパラメータに対する解釈が楽しいかもしれません。明確に人間の意思を載せてあるパラメータですから(それが物理的にどのような意味があるかは別として)。
とは言っても、やっぱディープラーニングは強いので上手く融合したようなモデルが欲しい。となると深層生成モデルをやるしか無いのか(今のとこ必要性が…。しかしモチベーションが楽しさってのも幸せなのかもしれない)。