KL reverseとKL forwardのメモ

はじめに

確率分布間の隔たりを測る尺度であるダイバージェンス $D[p : q]$ は一般的に対称性を有していません。 したがって、 $D[p : q]$ と書いたときには言葉としては「$p$ から $q$ へのダイバージェンス」と読まなければいけません。当然のことながら $p$ から $q$ と $q$ から $p$ へのダイバージェンスの値はそれぞれ違います。

今回はダイバージェンスとして最もよく知られているKLダイバージェンスについて、 $p$ から $ q $ へのKLダイバージェンスとその逆についてメモを残しておきます。

KLダイバージェンス

表記に関する注意事項

$D [p: q]$ というダイバージェンスの書き方をするときに $KL[p : q]$ のことを KL forward 、$KL[q : p]$ のことを KL reverse と表記されているケースが英語の文献だと見られました。「前とか後ろとか、そんなのどっちを基準にするかの認識が統一されてなきゃ難しいので、素直に数式で書けば良くない？」と思うのですが、どうもちゃんと認識が統一されているようでございます。

要確認なのですが、どうやら $p$ のことを理想的な分布、あるいは真の分布として扱っており、$q$ の方をこれから $p$ に近づけていく近似分布（サンプリングに使うような分布）であることを意識しているようです。

具体的に変分推論の例を上げれば、通常、本来の事後分布 $p(Z \mid X)$（あるいはその正規化されていない分布、すなわち同時分布 $p(X, Z)$ ）の方を $p$ として、こいつに近づけていきたい変分モデル $q(Z ; \eta)$ を $q$ と書く慣習に習っているようです。

変分推論では $KL[q(Z; \eta):p(Z\mid X)]$ を最小化しようとするので、KL reverseを使うという表記がなされたりします（やっぱり混乱するから数式で書いてほしいですね）。ひとまず、そのような用語があるということは知っておいて損はないかと思います。もしも私に認識の間違いがありましたら一報ください。

確率分布間の比較

今回は正規分布を使ってKL forward と KL reverseの比較をしてみたいと思います。 使う分布は下記の3つ。

$$ \begin{align} N(0, 1) \\ N(0, 2) \\ N(1, 1) \end{align} $$

です。図示をすると以下のようになります。

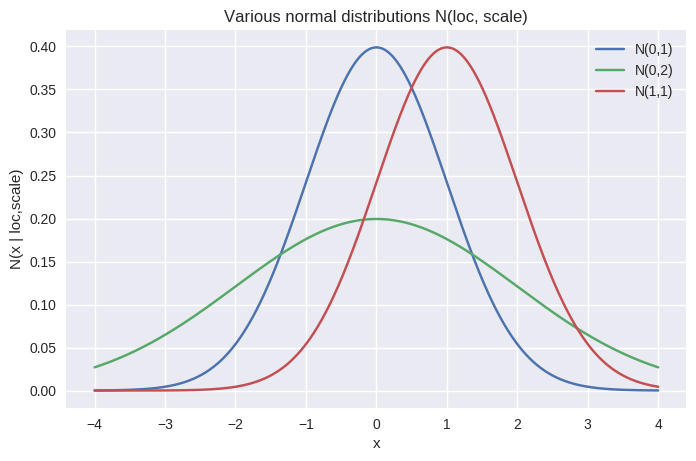
一旦考えてほしいのは、標準正規分布 $N(0, 1)$ と比べてより近いのは $N(0, 2)$ なのか $N(1, 1)$ なのかということです。基本的な統計パラメータの空間での幾何学（情報幾何学）の復習になりますが、素朴なパラメータの距離空間を使ってしまうと $(\mu, \sigma)$ という座標を取り、 $(0, 1)$ と $(0, 2)$ の距離、 $(0, 1)$ と $(1, 1)$の距離をユークリッド距離で比較したくなってしまうかもしれません。この場合、偶然にも（というより、そう選んでいるのだが）両者の距離は等しいということになってしまいます。

しかし確率分布の形からどちらが近いだろうか…？ということを考えたときに、平均のずれと標準偏差のずれを対等に扱って良いかは自明ではありません。もちろんそれはおかしいので、ちゃんとした計量を入れたいということになり、「KLダイバージェンス」が使えるということになったのです。

ダイバージェンスの非対称性

確率分布間の距離を測りたいと言いながら、ダイバージェンスは一般には非対称であるので、実はどちらから測るかをちゃんと意識しなければなりません。今回は KL forward と KL reverse で先程の正規分布間のダイバージェンスを調べてみます。

まず、変分推論のノリで、本来の形状が $N (0, 1)$ であるときに、近似分布の候補として $N(0, 2)$ と $N(1, 1)$ を準備し、 KL reverse で測ってどちらが近似分布として妥当なのかを見てみましょう（注意として、本来正規分布を正規分布で近似推論するようなことはありません。近似でも何でもなく正確に求まるからです。近似推論を使うのは $p$ が複雑で解析的に形状がわからないときに、 $q$ からのサンプリング値を使って $p$ に近いサンプリングが KLダイバージェンスの意味で出来ているかを見てみようというモチベーションになります。また今回のケースはサンプリングを取って測らなくても数式として計算できます。ただ、一般的な統計・機械学習での利用用途も踏まえて下記の方法を使います）。

KL reverseの計算

ライブラリとして TensorFlow Probabilityを利用します。

tfp.vi.monte_carlo_csiszar_f_diverfence()関数を使うと、用いたいダイバージェンス、近似したい対称の分布 $p$ （の対数尤度関数）と近似モデル $q$ を指定して $q$ からのサンプリングを取ってきてダイバージェンスを計算してくれます。まずは KL reverse （ $KL(q: p)$） を使います。

import tensorflow as tf
import tensorflow_probability as tfp
import numpy as np
import matplotlib

def kl_reverse(p, q):
    return tfp.vi.monte_carlo_csiszar_f_divergence(
        f=tfp.vi.kl_reverse,
        p_log_prob=p.log_prob,
        q=q,
        num_draws=100000
    )

上記の num_draws は許す限り大きいほうが正確でしょう。 近似分布 $q$ の形状を再現するのに十分な数を準備しましょう。 あとは下記のコードのように分布を準備して、ダイバージェンスを計算してもらいます。

normal_standard = tfd.Normal(0, 1)
normal_bigscale = tfd.Normal(0, 2)
normal_shiftloc = tfd.Normal(1, 1)


standard_to_standard = kl_reverse(normal_standard, normal_standard)
bigscale_to_standard = kl_reverse(normal_standard, normal_bigscale)
shiftloc_to_standard = kl_reverse(normal_standard, normal_shiftloc)

これらの値を見て見ると下記のようになりました。

print("standard_to_standard :", standard_to_standard.numpy())
print("bigscale_to_standard :", bigscale_to_standard.numpy())
print("shiftloc_to_standard :", shiftloc_to_standard.numpy())

## standard_to_standard : 0.0
## bigscale_to_standard : 0.8097206
## shiftloc_to_standard : 0.49300173

パラメータ空間においてユークリッド距離をいれてしまうと $N(0, 1)$ と $N(0, 2)$ の距離と$N(0, 1)$ と $N(1, 1)$ の距離は同じでしたが、 $KL(q:p)$ によると、 $N(0, 1)$に近いのは $N(1, 1)$ の方であるという結論になりました。しかし

なるほど、では同じくらいずれるのであれば、標準偏差に比べて平均のズレの方がマシなんだ！！というのは間違いです。

KL forwardの計算

ダイバージェンスの非対称性を思い出してください。単に値が forward と reverse 一致しないというだけではありません。結論から言えば、今回の場合は、その大小まで逆転してしまいます。

def kl_forward(p, q):
    return kl_reverse(q, p)

standard_to_standard = kl_forward(normal_standard, normal_standard)
standard_to_bigscale = kl_forward(normal_standard, normal_bigscale)
standard_to_shiftloc = kl_forward(normal_standard, normal_shiftloc)

print("standard_to_standard :", standard_to_standard.numpy())
print("standard_to_bigscale :", standard_to_bigscale.numpy())
print("standard_to_shiftloc :", standard_to_shiftloc.numpy())

## standard_to_standard : 0.0
## standard_to_bigscale : 0.31781003
## standard_to_shiftloc : 0.50057

こちらの測り方では、標準偏差のズレに対して寛容になっています。一体何が起こっているのでしょうか。KLダイバージェンスの数式を計算したらそうなるからそうである、と言えばそれでオシマイなのですが、直感的にこれらの測り方の違いはどこにあるのでしょうか。

確率分布の形状再考

再び下記の図を見ましょう。どのように値を測っているのかを、パラメータ空間で議論するのが情報幾何学ですが、今回は我々が可視化できるデータの空間で直感的に把握することを目指します。

今、変分推論のように $p$ を近似するために $q$ を準備していい感じの $q$ を選びたいというモチベーションを心に持ってください。 $N(0, 1)$ を近似したいときに、$N(1, 1)$ が相応しいと思いますか？ $N(0, 2)$ が相応しいと思いますか？今回の例では、それが forwardかreverseかで変わってしまうという奇妙な話を見てしまっているのです（ちなみに大げさに一方を標準正規分布と似つかない分布にすれば、reverseで測っても forwardで測っても、値の違いはあれど大小が逆転したりはしません）。

この話を見るために、もっと分かりやすい例を見ます。

近似分布の候補はそのままに、近似したい元々の分布を混合正規分布にしてみます（青色）。

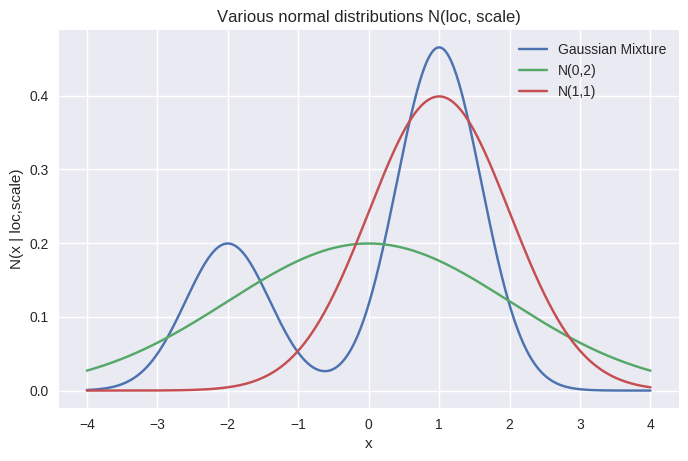
さて、近似分布として選ぶならば、赤色か緑色どちらが相応しいでしょうか。赤色は混合正規分布の大きい方の山を抑えていますが、他方の山を完全に捨てる形になります。緑色は両方の可能性を捨てずに取っていますが、いずれの山の形状も表現できていません。

実はこれも、結論から言えば、reverseで測るのか forwardで測るのかでダイバージェンスの値の大小が変わります。

gm_to_gm = kl_reverse(gm, gm)

bigscale_to_gm = kl_reverse(gm, normal_bigscale)
shiftloc_to_gm = kl_reverse(gm, normal_shiftloc)
gm_to_bigscale = kl_forward(normal_standard, gm)
gm_to_shiftloc = kl_forward(normal_standard, gm)

print("standard_to_standard :", standard_to_standard.numpy())
print("bigscale_to_gm :", bigscale_to_gm.numpy())
print("shiftloc_to_gm :", shiftloc_to_gm.numpy())
print("gm_to_bigscale :", gm_to_bigscale.numpy())
print("gm_to_shiftloc :", gm_to_shiftloc.numpy())

## standard_to_standard : 0.0
## bigscale_to_gm : 1.2940234
## shiftloc_to_gm : 0.34400007
## gm_to_bigscale : 0.89577323
## gm_to_shiftloc : 0.9020508

結果として、KL reverseは高い方のピークをガッチリ掴んでいる赤色の山のほうが分布として近しいと結論しています。他方KL forwardはどっちつかずな値になりつつも、まあ、まだ緑色の方がマシかな？くらいの結論です。

変分推論では KL reverseを利用する

ところで、仮に近似分布として緑が選ばれた場合、本来仮定されていた混合正規分布ではほとんど生じないはずの $0$ という値が最もサンプリングされる分布になってしまいます。これは、データを表現する分布として明らかに不適切ではないでしょうか…？私達は左側の小さいピークを捨ててでも、忠実に右側の大きいピークを掴み、データを発生させてくれる近似分布を選びたいはずです。

したがって 変分推論では KL reverseを利用します。

直感的な理解としては

• KL forwardは近似対象の分布 $p \neq 0$ の領域を $q$ で網羅しようとします
• KL reverse は近似対象 $p$ の際立った部分を $q$ で捉えに行こうとし、結果 $q$ の分散は一般に小さくなります

KL reverse で変分推論をするときは、計算可能な限り変分モデルの表現力を高めましょう。過学習自体はそもそも自分が立てた $p(X \mid Z)$ とその事前分布 $p(Z)$ を考える時点で意識するものであり、そういう分布なのだと仮定した以上は、しっかりその仮定した分布を求めたいはずです。したがって仮定した分布を近似するときに妥協などは要りません。

今回も、当然、近似分布 $q(Z)$ として混合正規分布を選んでしまえば上手く行く話です。もちろん通常の変分推論を使うような問題では、そもそも計算ができなさそうな $p(X\mid Z)$ と $p(Z)$ の組になってしまうので、自ずとこれよりも制限された $q(Z)$ を選ばざるを得ない状況になっているはずです。