はじめに
数式の表示がされるかテストも兼ねて、ベイズの定理を使わず事後分布の推論の話をします。
グラフィカルモデリング
グラフィカルモデルと同時分布
確率モデリングをしていく上で、非常に便利に使える道具としてグラフィカルモデルを簡単に導入しておきます。 難しい話はしません。単にツールとして数式の代わりにグラフィカルモデルを「読める」ようにしておくと便利というだけの話です。
同時分布 $p(a, b, c)$ というものを扱う場合、そのグラフィカルモデルの出発点は下記のようになります。

これは無向グラフなどと呼ばれますが、兎にも角にも同時分布はこのように全ての確率変数を対等に扱ったグラフになっていることに注目しておきましょう。ここからモデリングを行います。
まず、確率分布にいつでも成り立っている、同時分布と条件付き分布の関係式を見ましょう。
$$ p(a, b, c) = p(a \mid b, c)p(b, c) $$
難しく感じるでしょうか。変数が2つならよく知っている式ですね。
$$ p(x, y) = p(x\mid y)p(y) $$
こうしておいて $x = a$ と $y = (b, c)$ という具合に代入してしまって$p(a, b, c) = p(a \mid b, c)p(b, c) $ と書き換えたと考えるのがひとまず覚えやすいでしょう。すると、グラフィカルモデルとしては下記のようになります。

これは単に、確率分布の数式から見れば同値変形です。しかし、グラフィカルモデルでみると矢印が追加されています。条件付きの $a$ が $b, c$ から生成されているように描かれていることに注意しましょう。ところで
$$ p(a, b, c) = p(a \mid b, c)p(b, c) = p(a \mid b, c)p(b \mid c) p(c) $$
と最右辺まで変形できることに注意しましょう。そうするとグラフィカルモデルは

となります。これもまた、同時分布を常に成り立っている関係式で変形したにすぎない代物ですが、やはりグラフィカルモデルで見ると矢印が追加され別物に見えますね。当然今回みた2つの有向グラフは、矢印の向きを変えて(すなわち変数の立場を入れ替えて)も構いません。いつでも同時分布と条件付き分布の関係式を思い起こせばそれは単なる同値変形なのですから。
裏を返せば、この手のグラフィカルモデルは全部実質同じであるので、どんな矢印の付け方をしたところで(人間がこの画をみたときの印象以外に)モデリングをしたことにはなりません。グラフィカルモデリングは、確率変数間のつながりを断ち切ることで実施します。
グラフィカルモデリング
例えば下記のグラフィカルモデルを見てみましょう。

このモデルは $b, c$ に繋がりがなくなっています。この場合、このグラフィカルモデルを表現する数式は
$$ p(a \mid b, c)p(b)p(c) $$
となります。$b$ と $c$ はだれからも条件付けられていません。
これはいつでも成り立っている
$$ p(a, b, c) = p(a \mid b, c)p(b, c) $$
に対して、$b$ と $c$ は独立であるというある種の特殊性を入れることで $p(b, c) = p(b)p(c)$ という独立な確率変数で成り立つ式(というよりか定義)を使い、
$$ p(a, b, c) = p(a \mid b, c)p(b, c) = p(a \mid b, c)p(b)p(c) $$
と同時分布をモデリングしたことになります。この変形は独立という制限を人間が外部から加えてやらなければできない変形です。いつでも成り立っている式を、わざわざ壊して、特殊なときにしか成り立たない式に変形したのです。私達はデータ(あるいは事前知識)と向き合って $b$ と $c$ の間にそういう関係がありそうだと思ったからそうするのです。故にモデリングしたことになるのです。
下記のようなモデリングも考えられます。$c$ が $a$ と $b$ に影響を及ぼしているような様子です。
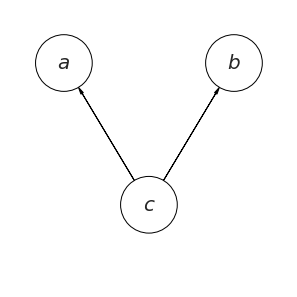
この場合には同時分布を下記のように変形したことになります(中辺に注意してください。これまでと、変形の手順が若干異なります。変形の仕方に任意性があることを忘れないでください)。
$$ p(a, b, c) = p(a, b \mid c)p(c) = p(a\mid c)p(b \mid c)p(c) $$
これは $a$ と $b$ が $c$ のもとで条件付き独立であると言います。これも最右辺は条件付き独立であるという特殊性を導入することで実施した式変形であることに注意してください。これもまたモデリングの1つの方法というわけです。
まとめ
さあ、ここまででなんとなく、「数式上で議論するのと、想定しうる確率変数を全て書き下した無向グラフから始めて、繋がりを切ったり方向性を付けたりするグラフィカルモデリング、どっちがプロトタイプに向いているだろうか?きっとグラフィカルモデルの方が直感的で説明しやすいだろう」と思うわけです。
最近、グラフィカルモデルの理論を使った様々な解析の話を展開する用途ではなく、単に自分はどんなモデリングしたのかを示すためにグラフィカルモデルが掲載されているケースが多々あります。是非「読める」ようになりましょう。
正規分布のパラメータの事後分布
さてデータ $y$ が正規分布 $\mathcal N (y \mid \mu, \sigma)$ から発生していると考えているとしましょう。このモデルにおいてベイズ推論を行う場合、$y$ に ${\rm i.i.d}$ を仮定して、$Y = (y _ 1, \cdots, y _ N)$ という $N$ 個の $y _ i$ を考え
$$ \begin{align} p(\mu) &= {\rm Normal}(\mu \mid 0, 10000) \\ p(\sigma) &= {\rm HalfCauchy}(\mu \mid 0, 5) \\ p(Y\mid \mu, \sigma) &= \prod _ {i=1} ^N {\rm Normal}(y _ i, \mu, \sigma) \end{align} $$
と事前分布と尤度関数を決めることによって推論を進めたりします。
ここで一旦立ち止まって、先程までみた同時分布のグラフィカルモデルによるモデリングの話を思い出しましょう。ひとまず、いま確率変数であると思っているものが $y _ 1, \cdots y _ N, \mu, \sigma$ とあるわけです。これらの同時分布 $p(Y, \mu, \sigma)$ を作る際に
$$ p(Y, \mu, \sigma) = p(Y \mid \mu, \sigma)p(\mu, \sigma) = p(Y \mid \mu, \sigma)p(\mu)p(\sigma) $$
と式変形してみましょう。中辺までは常に成り立っている式であり、右辺は $\mu$ と $\sigma$ が独立であるという特殊性を入れています(グラフィカルモデルの基本のところで見た変形です)。続いて更に特殊性を追加します。 $y _ i$ という確率変数が $N$ 個観測されるという話において、 $y _ i$ が互いに $\mu, \sigma$ に関して条件付き独立 であれば
$$ \begin{align} p(y _ 1, \mu, \sigma) &= p(y _ 1 \mid \mu, \sigma)p(\mu)p(\sigma)\\ p(y _ 2, \mu, \sigma) &= p(y _ 2 \mid \mu, \sigma)p(\mu)p(\sigma)\\ p(y _ 3, \mu, \sigma) &= p(y _ 3 \mid \mu, \sigma)p(\mu)p(\sigma)\\ &\vdots \\ p(y _ N, \mu, \sigma) &= p(y _ N \mid \mu, \sigma)p(\mu)p(\sigma) \end{align} $$
の掛け算によって
$$ p(Y\mid \mu, \sigma) = \prod _ {i=1} ^N {\rm Normal}(y _ i, \mu, \sigma) $$
と表現できます。これは、グラフィカルモデルとしては

となっています。ここで $y$ が黒く塗りつぶされているのは観測可能な確率変数であることを表しています。端的に観測データと思ってもらって構いません。更に四角い枠に囲まれているのは、 $\mu, \sigma$ に条件付けられた $y$ が $N$ 個手に入っていますよ、という話をわざわざ $N$ 個の $y$ を書き下すのは紙面の無駄ということで、このような表現が行われます。通常プレート表現と言います。上にある黒点と分布が文字で書かれているのは、俗に言う事前分布とハイパーパラメータを明示するための表現で、必ずしも描かれているものではありません。
さてここまで見てみると、普通に実施される正規分布での推論は、なんだかグラフィカルモデルを1から作ってみると随分と特殊な仮定が散りばめられていたことに気づくはずです。すると、「$\mu$ と $\sigma$ が独立であるという仮定は本当にいるのか?」とか「各データは本当に独立であると思って良いのだろうか」とか色々思うところが出てくるはずです。
続いて、推論をしようという場合には、すでに手元に入っている観測データ $Y$ を使ってどうにか観測できていない $\mu, \sigma$ について知ってやろうと思うわけです。この時、同時分布の変形には任意性があったことを思い出してください。
$$ p(Y, \mu, \sigma) = p(\mu, \sigma \mid Y)p(Y) $$
という変形をしてもよく、しかもこれは「常に」成り立っています。ところで我々がモデル化した($\mu, \sigma$ の独立という特殊性も考慮した変形を含む)同時分布は
$$ p(Y, \mu, \sigma) = p(Y \mid \mu, \sigma)p(\mu)p(\sigma) $$
だったのでした。さあ、ここまでこれば、「いつでも成り立っている同時分布の変形」と「我々がモデル化した特殊な同時分布」を繋げてやるだけです。
$$ p(\mu, \sigma \mid Y)p(Y) = p(Y \mid \mu, \sigma)p(\mu)p(\sigma) $$
ちょうど、左辺の $p(\mu, \sigma \mid Y)$ の部分が、観測できている $Y$ に条件付けられた $\mu, \sigma$ の分布になっているので(というよりそうなるように変形した)、これに着目することにすれば
$$ p(\mu, \sigma \mid Y) = \frac{p(Y \mid \mu, \sigma)p(\mu)p(\sigma)} {p(Y)} $$
と表すことができ、この式に具体的な分布の式を代入して解けば、$\mu, \sigma$のことを少しは知ることができるだろうというわけです。これは俗に言う、事後分布であり、ベイズの定理でサッと出してしまうことが多いものです。しかしここまでみたとおり、確率変数と考えたものたちの関係性の整理と、同時分布と条件付き分布の関係だけで記述ができる話だったのです(というよりも、それらを丁寧に見ないと、実はええかげんなモデリングになっていたりする)。
そういえば $Y = (y _ 1, \cdots, y _ N)$ の各 $y _ i$ も$\mu, \sigma$ に関して条件付き独立であったことを思い起こせば最終的には
$$ p(Y \mid \mu, \sigma )\prod _ {i=1} ^N {\rm Normal}(y _ i, \mu, \sigma) $$
も代入できるわけですが、まあそれは面倒なので辞めておきましょう(このようにデータが $i.i.d$ という話は本来最後の最後に先延ばしても良いはずのものであり、それを仮定せずとも色々な議論ができる。が、たいてい簡単のため、最初に宣言されることが多い)。
回帰問題のモデリング
書くかもしれないし書かないかもしれない。
とりあえずテスト投稿。