JAXとPyTorchで勾配法とニュートン法を試す

はじめに

最近、しっかり学ぶ数理最適化を購入しました。

しっかり学ぶ数理最適化 モデルからアルゴリズムまで (KS情報科学専門書)

1章→3章と読んでいく中で、元々馴染みの深い連続最適化の極々基本的な手法である勾配法とニュートン法を試してみました。実装はJAXを使っています。こいつは現状、最高の自動微分ライブラリだと思っております（深層学習ライブラリという観点ではPyTorchの方が今の所使いやすい）。

普通、機械学習では二次微分なんてパラメータが多すぎてまともに計算できる見込みがないので、純粋なニュートン法なんて絶対に使わないのですが、その圧倒的な性能の高さを確認し、兎にも角にも勾配法の弱さを確認しておこうと思います。

と言いつつ、勾配法は収束が弱いのだが、機械学習や統計のパラメータ推定問題において微分可能な損失関数の最小化が本当の意味での目的関数になっているわけではない。実際にはデータの背後に潜む真の分布との誤差や、未来のデータの予測性能に対する誤差を小さくしたいのであって、表層上代理で解かれている問題が（問題の枠組みの中での）真の解に辿り着くことは、参考にはなるが本質的に求めたいものではない。という意味で、別に収束して貰わなくても構わないというところはある。実際、有限個データでニューラルネットのパラメータを最尤推定しても、そもそもニューラルネットに対して最尤解にさほど意味はない。cross-validation等の検証の結果がほぼ全てである。最適化方面から見たら悪名高い early stopping も確かにその手法の良さを測る根拠自体は乏しいかもしれないが、現実問題、おそらく意味のあるsolution になっているだろうと思われる。

PyTorchのコードを追加 したことでこの手の計算を生で書く場合のJaxの利便性も見ます。 PyTorchはtorch.nn.Moduleクラスやtorch.optimモジュールによって計算グラフの管理がそこそこ隠蔽されているため、普段は意識することがありませんが、若干生のAPIは奇妙な形式になっていたりします。

逐次更新による最適化

大枠

最小化問題に関して動かすパラメータを $\bf x$ とします。目的関数 $ f (\mathbf x) $ に対して

$$ y _ 0 = f (\mathbf x _ 0) $$

をひとまず評価しておき、

$$ \mathbf x _ {1} \leftarrow \mathbf x _ 0 + \mathbf d _ 0 $$

と更新をしてみます。この更新後の $\mathbf x _ {1}$ を $y _ 1 = f(\mathbf x _ 1)$ と評価してみて、$y _ 1 < y _ 0$ になっていれば嬉しいはずであり、このような更新 $\mathbf d _ i$ を適宜決め

$$ \mathbf x _ {i + 1} \leftarrow \mathbf x _ i + \mathbf d _ i $$

と更新していく方法が逐次更新による最適化の一形態になります。

勾配法

数式

ここで どんな $\mathbf d _ i$ を設定するのかが重要ですが、勾配法と呼ばれる手法はその名の通り、

$$ \mathbf d _ i = - \alpha _ i \nabla f (\mathbf x _ i) $$

と、目的関数の現在のパラメータ $\mathbf x _ i $ における勾配を計算し、$f$ が減少する方向を更新方向とします。 ここで $\alpha _ i > 0$ です。これがなぜ目的関数を減少させる方向であるのかの大枠は、目的関数についてのテイラー展開すると

$$ f(\mathbf x + \mathbf d ) = f(\mathbf x) + \nabla f(\mathbf x) ^ T \mathbf d + o(\mathbf x ^ 2) $$

となっており、これは $ || \mathbf d ||$ が小さい範囲での関数 $f(\mathbf x)$ の一次近似となっています。近似ができていることを信じれば、この $\mathbf d$ として何か適当な値を動かしてみたときに $f (\mathbf x + \mathbf d) - f (\mathbf x)$ が増えるか減るかを見積もることができます。これは上記の近似の第一項を左辺に移動すれば

$$ f (\mathbf x + \mathbf d) - f (\mathbf x) = \nabla f(\mathbf x) ^ T \mathbf d + o(\mathbf x ^ 2) $$

と表記できます。さて、このときの右辺が負になってくれれば $\mathbf d$ だけ動かしたときに減少したと言えます。そして願わくばその減少が大きいと嬉しいですね。今 $ \nabla f(\mathbf x) ^ T \mathbf d $ は内積の計算であり、内積の値の絶対値は、方向が揃っていたほうが大きいはずです。従って、 $\mathbf d $ として $\nabla f(\mathbf x)$ という方向を取ることで決定します。

次に符号ですが、同じベクトル同士で内積を取ると、それは二乗ノルムになり、正の値になります。今は値を減少させたいのですから右辺は負になっているべきであり、$\mathbf d$ の符号は $\nabla f(\mathbf x)$ とは逆向きにすることにします。

最後に、このテイラー展開は $ || \mathbf d ||$ が小さな範囲でしか成り立たない近似です。$\nabla f(\mathbf x)$ という勾配ベクトルが小さなノルムになっているかは定かではありません。従って、近似が成り立つ小さな範囲に $\mathbf d $ を押し止めるために $\alpha$ という小さな正の値を準備します。

そうすることで

$$ \mathbf d _ i = - \alpha _ i \nabla f(\mathbf x _ i) $$

という更新の仕方を決めることができました。$\alpha _ i$ はパラメータ $x _ i $ の値（あるいはその勾配）に依存して変える必要があります（なぜならテイラー展開で近似が成り立つ範囲が場所によって異なるから）。また、最適化の観点でいうと、近似が成り立つ範囲の中でも1回のステップでなるべく大きく値を小さくしたい、すなわち線形近似された空間でなるべく更新幅 $\mathbf d _ i$ を大きくしたいという欲張りな思いもあります（ $\alpha$ がかなり小さければ近似は成り立たせられるが、最適化の計算量を小さくしたいので、行けるとこは粗っぽく行きたいのだ）。

というわけで、$\alpha _ i$ の決め方も本当なら色々あるのですが、今回の例では定数決め打ちでいきます。

勾配法コード例

まずは必要なライブラリをインポートしておきます。

import jax
import jax.numpy as jnp
from jax import value_and_grad, jit

import matplotlib.pyplot as plt
import numpy as np

次に目的関数を可視化しておきます。ついでに、最適化を始める初期値の点もプロットしておきましょう。

def objective(x):
    f = x[0]**4 + 2*x[0]**3 + 3*x[1]**2 + 2*x[0]*x[1] - x[1]
    return f

x1 = np.linspace(-4, 4)
x2 = np.linspace(-4, 4)
xx1, xx2 = np.meshgrid(x1, x2) 
f = objective([xx1, xx2])

x_init = jnp.array([3., 3.])
f_init = objective(x_init)

plt.figure(figsize=(7,7))
plt.contourf(xx1, xx2, f, cmap='Blues')
plt.scatter(x_init[0], x_init[1], c="r", s=100)

さてこの状態から勾配法で値を更新していきます。今回の目的関数は4次であり、実はところどころ勾配が小さくなっているようなところがあります。今回適当な終了条件で勾配法がどこに収束するかを確認します。ちなみに Jaxは関数型で設計された機能が多く、例えば jax.value_and_grad はpython関数を引数に取り、python関数を戻り値にする関数です（というわけで下記では横着してますが、value_and_grad はループの外で書いて、勾配と評価値を返す関数を定義しておいて、ループの中でその関数を呼ぶとすべき。また、ループの外で定義するときは純粋関数ならばjax.jit でコンパイルしたほうが良い。今回は最適化法の説明のためプログラムの細かいところはなるべく少なくなるように書いた）。

#############################
#  JAX
#############################
x = jnp.array([3.0, 3.0])
tmp_val = 1e5

x_list = [x]

while True:
    val, grad_val = value_and_grad(objective)(x)
    x = x - 1e-3*grad_val
    x_list.append(x)
    if jnp.abs(val - tmp_val).sum() < 1e-3:
        break
    tmp_val = val

#############################
#  PyTorch
#############################
x = torch.tensor([3.0, 3.0], requires_grad=True)
tmp_val = 1e5

## numpyに変換された値のコピーを保存
x_list = [x.detach().numpy()]

while True:
    val = objective(x)
    ## tuple で返ってくる 
    grad_val = ag.grad(val, x)[0]
    x = x - 1e-3*grad_val
    ## x 計算グラフを切ってnumpyに変換された値のコピーを保存
    x_list.append(x.detach().numpy())
    if torch.abs(val - tmp_val).item() < 1e-3:
        break
    tmp_val = val

# 可視化は共通

plt.figure(figsize=(7,7))
plt.contourf(xx1, xx2, f, cmap='Blues')
for i, x_trj in enumerate(x_list):
    plt.scatter(x_trj[0], x_trj[1], c="r", s=80)
    if i == len(x_list) - 1:
        plt.scatter(x_trj[0], x_trj[1], c="g", s=80)
        plt.title(f" iter: {len(x_list)} solution : {val}")

さて、3桁を超えるiterationの末にある値に収束したようです。図を見ると、各点で等高線を下っていってるのが分かります。

ちなみに速度は圧倒的にPyTorchの方が速いです。

Eager evaluationでPythonの世界で戦っている限り、計算グラフ周りがC++で書かれているPyTorchに軍配が上がります。しかし、jaxのコードで value_and_grad(objective)(x) と書かれている部分は、Pythonにvalue_and_grad(objective) をループの中で何度も評価させる必要はありません。これをループの外に出して、予め v_and_g = jit(value_and_grad(objective)) とコンパイルしておきます。すると、同等の速度になります。

x = jnp.array([3.0, 3.0])
tmp_val = 1e5

x_list = [x]

v_and_g = jit(value_and_grad(objective))

while True:
    val, grad_val = v_and_g(x)
    x = x - 1e-3*grad_val
    x_list.append(x)
    if jnp.abs(val - tmp_val).sum() < 1e-3:
        break
    tmp_val = val

ニュートン法

数式

次はニュートン法です。ニュートン法では更新 $\bf d _ i$ を

$$ \mathbf d _ i = - \alpha _ i \{\nabla ^ 2 f (\mathbf x _ i)\} ^ {-1} \nabla f(\mathbf x _ i) $$

と取ります。いい加減にしてくれ、という感じかもしれませんが上記勾配法を理解している上で説明します。

まず勾配法では、一次近似して、$f (\mathbf x + \mathbf d) - f (\mathbf x)$ が負になるように更新 $\mathbf d$ を決めたのでした。次は横着せず二次近似してみましょう。

$$ \begin{align} f (\mathbf x + \mathbf d) - f (\mathbf x)& = \nabla f(\mathbf x) ^ T \mathbf d + o(\mathbf x ^ 2) \\ &= \nabla f(\mathbf x) ^ T \mathbf d + \frac{1}{2} \mathbf d ^ T \nabla ^ 2 f(\mathbf x) \mathbf d ^ T + o(\mathbf x ^ 3) \end{align} $$

と $o(\mathbf x ^ 2)$ に隠れていた二次の項を取り出しました。二次の項を使うと少なくとも $\mathbf x ^ 2$ の近傍で停留点が得られます（二次関数として切り出したのだから、勝手に二次関数の適用範囲を広げればどこかに極値がいるというわけだ。すなわち $\mathbf d$ の方を勝手に新しい座標として動かすときに、その二次関数で切り出した空間で行けるとこまで行っちゃえという精神である）。

このことは

$$ f (\mathbf x + \mathbf d) = f (\mathbf x) + \nabla f(\mathbf x) ^ T \mathbf d + \frac{1}{2} \mathbf d ^ T \nabla ^ 2 f(\mathbf x) \mathbf d ^ T + o(\mathbf x ^ 3) $$

を $\mathbf d$ で微分して $ 0 $ となる条件を見つければ良く、

$$ \nabla _ d f(\mathbf x + \mathbf d) = \nabla f (\mathbf x) + \nabla ^ 2 f (\mathbf x)\mathbf d = 0 $$

が勝手に作った二次関数の$\mathbf d$ による勾配が $0$ になる条件であり、これを解けば $\mathbf d$ を動かすだけ動かした末に一番底になる値を（二次近似の範囲で）直接見つけたことになります。

なぜ勾配法でこれができなかったのだろうか。それは勾配法は一次近似であり、この近似された空間の中では $\mathbf d$は動かせば動かすほどいくらでも値を小さくできてしまうからである。二次近似によって、勝手に近似した空間の中に初めて停留点が生まれた。この近似空間の停留点まで直接移動してしまうことで（当然、本当の目的関数からは剥離があるのだろうが）、速く収束できるのではないかという作戦だ。

そのような停留点は上記式の中間辺と最右辺

$$ \nabla f (\mathbf x) + \nabla ^ 2 f (\mathbf x)\mathbf d = 0 $$

を $\mathbf d$ に関して解いて、

$$ \mathbf d = - \{ \nabla ^ 2 f(\mathbf x) \} ^ {-1} \nabla f(\mathbf x) $$

と求まります。従って、目的関数を二次近似した空間で停留点を求め、その点を次の値にしてしまうという更新則を採用するのであれば上記の式が更新則になります。無論、二次近似は停留点があるから、ひとまず次の移動先の候補を上記のように求められるというだけで、そもそも二次近似を信じて良いのかは分かりません。各点 $\mathbf x _ i$ に応じてその曲率が異なることなどを考慮し、やはりステップ幅の調整係数を各点で導入し

$$ \mathbf d _ i = - \alpha _ i \{\nabla ^ 2 f (\mathbf x _ i)\} ^ {-1} \nabla f(\mathbf x _ i) $$

とするのが一般形式です。

今回は簡単のため、二次近似で停留点をたどる $\alpha _ i = 1.0$ というバージョンを確認します。ちなみに $\nabla ^ 2 f(\cdot)$ はヘッシアンで行列の形式を取ります。

ニュートン法のコード例

問題設定は勾配法と同様なので、最適化のコードのみ記します。

# JAX

x = jnp.array([3.0, 3.0])
tmp_val = 1e5

x_list = [x]

while True:
    val, grad_val = value_and_grad(objective)(x)
    H = jax.hessian(objective)(x)
    H_inv = jax.scipy.linalg.inv(H)
    x = x - H_inv @ grad_val
    x_list.append(x)
    if jnp.abs(val - tmp_val).sum() < 1e-3:
        break
    tmp_val = val

# PyTorch
x = torch.tensor([3.0, 3.0], requires_grad=True)
tmp_val = 1e5

## numpyに変換された値のコピーを保存
x_list = [x.detach().numpy()]

while True:
    val = objective(x)
    ## gradはobjectiveの出力値を入力値で微分するというAPI
    grad_val = ag.grad(val, x)[0]
    ## hessianはobjectiveを関数、入力を値を渡すAPI、返り値はtensor
    H = ag.functional.hessian(objective, x)
    H_inv = torch.inverse(H)
    x = x - H_inv @ grad_val
    x_list.append(x.detach().numpy())
    if torch.abs(val - tmp_val).sum() < 1e-3:
        break
    tmp_val = val



plt.figure(figsize=(7,7))
plt.contourf(xx1, xx2, f, cmap='Blues')
for i, x_trj in enumerate(x_list):
    plt.scatter(x_trj[0], x_trj[1], c="r", s=80)
    if i == len(x_list) - 1:
        plt.scatter(x_trj[0], x_trj[1], c="g", s=80)
        plt.title(f" iter: {len(x_list)} solution : {val}")

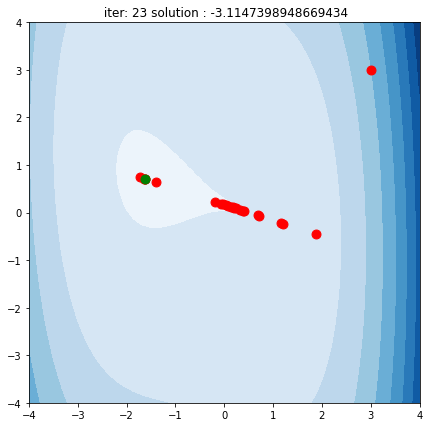
二次に情報がある分、勾配法より速く、そして正しい解にたどり着けています（勾配法のときの結果を見よ）。 また、最初のステップで、初期位置での二次近似を行い、その近似を信じて近似の世界の停留点までひとっ飛びしているのが見て取れます。その後最適解付近で行き来がありますがなんとか収束できているようです。

$\alpha _ i$ などの調整方法や、更にヘッセ行列退化問題などに対応する準ニュートン法、その他諸々最適化を学びたい方は私も勉強中である

しっかり学ぶ数理最適化 モデルからアルゴリズムまで (KS情報科学専門書)

をおすすめします。意外と平易な範囲の数学で読み進めやすいです（ただし、離散最適化の、あの頭を使う感じのアルゴリズム、僕は苦手だったりするのでそこは苦労しそう…）。